D - Multiset

Analysis

Let’s check when to output \(-1\) first.

Observation

The answer is \(-1\) if and only if the sum of elements of \(X\) and sum of elements of \(Y\) is different.

Proof

(\(\leftarrow\)) The operation \(-1\) at some index \(i\) and \({+1}\) at some index \(j\). This means that the sum of elements in the multiset remains unchanged. Therefore, it is impossible to make \(X = Y\) if their sum is different.

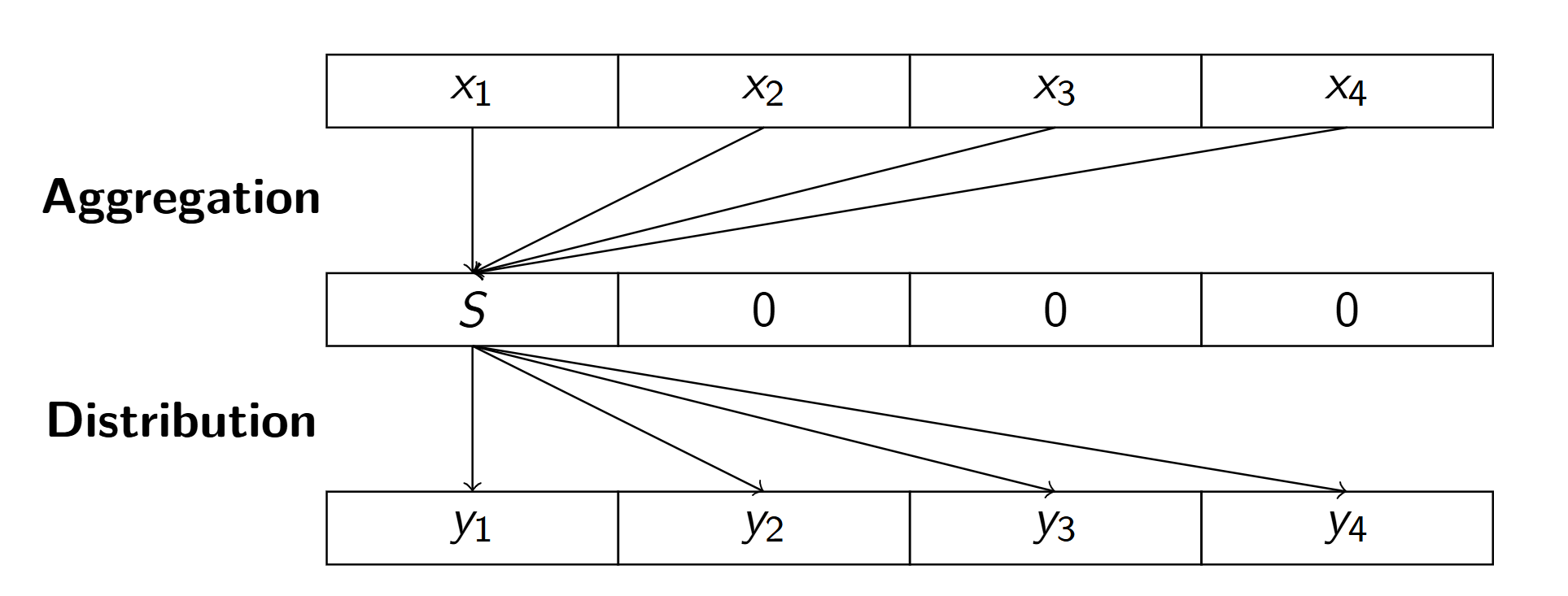
(\(\rightarrow\)) This proposition means that it is always possible to make them equal if the sum of elements is the same. One can just make all elements in \(X\) except the first one to be zero. By this, you can just always \(-1\) from the first index and \({+1}\) to the index \(j\) (for all \(j\)) \({y_j}\) times.

To find the minimum operations required, we can adopt a greedy strategy:

1. Sort both array in ascending order
2. The answer is \(\frac{1}{2}\sum_{i=1}^{n}{|x_i - y_i|}\)

Proof

From the previous observation, we know that it is possible only if the sum of elements of \(X\) and \(Y\) are the same.

Therefore, we can separate the operation \(-1\) and \(+1\) independently. That is, one operation is \(-1\) to some index \(j\) with cost \(\frac{1}{2}\) and another operation is \(+1\) to some index \(j\) with cost \(\frac{1}{2}\).

The problem is reduced to finding a one-to-one mapping between set \(X\) and set \(Y\).

• If \(x_i\) is mapped with \(y_j\), the cost is \(\frac{1}{2} \lvert y_j - x_i \rvert\).
• The cost of the mapping is \(\frac{1}{2} \cdot \sum_{\text{all mappings}}{\lvert y_j - x_i \rvert}\).

The optimal strategy is to choose the smallest \(x\) with the smallest \(y\). You may refer to some similar problems in Geekforgeek (Assign mice to holes). The proof is by case discussion. Please see (Li, 2016).

Codes

• C
• C++
• Java
• Python

• #include <inttypes.h>
  #include <stdint.h>
  #include <stdio.h>
  #include <stdlib.h>
  
  /**
   * Compare two integers.
   *
   * @param a First integer
   * @param b Second integer
   * @return Difference between the two integers
   */
  int compare(const void *a, const void *b) { return *(int *)a - *(int *)b; }
  
  /**
   * Finds minimum operations needed to make multiset X equal to multiset Y.
   *
   * An operation consists of choosing two elements in X and decrementing one
   * while incrementing the other by the same amount.
   *
   * @param n Size of the multisets X and Y
   * @param X First multiset of integers
   * @param Y Second multiset of integers
   * @return Minimum number of operations needed, or -1 if impossible. Note that
   * the answer may greater than 2^31-1, so we need to use int64_t.
   */
  int64_t solve(int n, int *X, int *Y) {
    qsort(X, n, sizeof(int), compare);
    qsort(Y, n, sizeof(int), compare);
  
    int64_t sum_X = 0;
    int64_t sum_Y = 0;
    for (int i = 0; i < n; i++) {
      sum_X += X[i];
      sum_Y += Y[i];
    }
  
    if (sum_X != sum_Y) {
      return -1;
    }
  
    int64_t operations = 0;
    for (int i = 0; i < n; i++) {
      operations += abs(X[i] - Y[i]);
    }
  
    return operations / 2;
  }
  
  int main() {
    int n;
    scanf("%d", &n);
  
    int *X = (int *)malloc(n * sizeof(int));
    int *Y = (int *)malloc(n * sizeof(int));
  
    for (int i = 0; i < n; i++) {
      scanf("%d", &X[i]);
    }
  
    for (int i = 0; i < n; i++) {
      scanf("%d", &Y[i]);
    }
  
    printf("%" PRId64 "\n", solve(n, X, Y));
  
    free(X);
    free(Y);
    return 0;
  }
  

• #include <algorithm>
  #include <cstdint>
  #include <iostream>
  #include <vector>
  
  class Solution {
   public:
    /**
     * Finds minimum operations needed to make multiset X equal to multiset Y.
     *
     * An operation consists of choosing two elements in X and decrementing one
     * while incrementing the other by the same amount.
     *
     * @param n Size of the multisets X and Y
     * @param X First multiset of integers
     * @param Y Second multiset of integers
     * @return Minimum number of operations needed, or -1 if impossible. Note that
     * the answer may greater than 2^31-1, so we need to use int64_t.
     */
    static int64_t solve(int n, std::vector<int>& X, std::vector<int>& Y) {
      std::sort(X.begin(), X.end());
      std::sort(Y.begin(), Y.end());
      int64_t sumX = 0, sumY = 0, moves = 0;
      for (int i = 0; i < n; ++i) {
        sumX += X[i];
        sumY += Y[i];
        moves += std::abs(X[i] - Y[i]);
      }
      if (sumX != sumY) {
        return -1;
      }
      return moves / 2;
    }
  };
  
  int main() {
    int n;
    std::cin >> n;
    std::vector<int> X(n), Y(n);
    for (int i = 0; i < n; ++i) {
      std::cin >> X[i];
    }
    for (int i = 0; i < n; ++i) {
      std::cin >> Y[i];
    }
    std::cout << Solution::solve(n, X, Y) << std::endl;
  
    return 0;
  }
  

• import java.util.Arrays;
  import java.util.Scanner;
  
  class Solution {
    /**
     * Finds minimum operations needed to make multiset X equal to multiset Y.
     *
     * An operation consists of choosing two elements in X and decrementing one
     * while incrementing the other by the same amount.
     *
     * @param n Size of the multisets X and Y
     * @param X First multiset of integers
     * @param Y Second multiset of integers to match
     * @return Minimum number of operations needed, or -1 if impossible
     */
    public static long solve(int n, int[] X, int[] Y) {
      // Implement your solution here
  
      Arrays.sort(X);
      Arrays.sort(Y);
  
      long sumX = 0;
      long sumY = 0;
      long ans = 0;
  
      for (int i = 0; i < n; i++) {
        sumX += X[i];
        sumY += Y[i];
        ans += Math.abs(X[i] - Y[i]);
      }
  
      if (sumX != sumY) {
        return -1;
      }
  
      return ans / 2;
    }
  
    public static void main(String[] args) throws java.lang.Exception {
      Scanner input = new Scanner(System.in);
  
      int n = input.nextInt();
  
      int[] X = new int[n];
      int[] Y = new int[n];
  
      for (int i = 0; i < n; i++) {
        X[i] = input.nextInt();
      }
  
      for (int i = 0; i < n; i++) {
        Y[i] = input.nextInt();
      }
  
      System.out.println(solve(n, X, Y));
      input.close();
    }
  }
  

• from typing import List
  
  
  class Solution:
      @staticmethod
      def solve(n: int, X: List[int], Y: List[int]) -> int:
          """
          Finds minimum operations needed to make multiset X equal to multiset Y.
  
          An operation consists of choosing two elements in X and decrementing one
          while incrementing the other by the same amount.
  
          Args:
              n (int): Size of the multisets X and Y
              X (list[int]): First multiset of integers
              Y (list[int]): Second multiset of integers to match
  
          Returns:
              int: Minimum number of operations needed, or -1 if impossible
          """
          X.sort()
          Y.sort()
  
          if sum(X) != sum(Y):
              return -1
  
          return sum(abs(x - y) for x, y in zip(X, Y)) // 2
  
  
  if __name__ == "__main__":
      n = int(input())
      X = list(map(int, input().split()))
      Y = list(map(int, input().split()))
  
      print(Solution.solve(n, X, Y))
  

References

1. Li, H. (2016). [HL-11] Connecting wires. In Github.io. https://hengfengli.github.io/algorithm/2016/05/30/hl-11-connecting-wires.html